"I imagine, therefore I am"
"Our imagination is stretched to the utmost,
not, as in fiction, to imagine things which are not really there, but
to comprehend things which are there."
- Richard Feinman, Physicist, Nobel Laureate
"To say prediction is the purpose of a scientific theory is to
confuse means with the ends.
It is like saying the purpose of a spaceship is to burn fuel."
- David Deutch, founding father of Quantum Computing, from 'The Fabric
of Reality'
An imagining, a theory, always awaits its double: the fact of its proof, as creation
St. Jerome as a virtual image, proscenium stage, still around today. |
Open windows, apertures, planes, perspective, the 'apprehension' of space, way back then. |
Hologram, as lens-less conjugate imaging, projecting disturbances of time in space as, real time interferometry, not shadows on a screen. |
| "The Mandelbrot set, named after Benoit Mandelbrot, is a fractal. Fractals are objects that display self-similarity at various scales. Magnifying a fractal reveals small-scale details similar to the large-scale characteristics. Although the Mandelbrot set is self-similar at magnified scales, the small scale details are not identical to the whole. In fact, the Mandelbrot set is infinitely complex. Yet the process of generating it is based on an extremely simple equation involving complex numbers." - David Dewey |
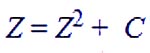
Mandelbrot
formula where |
Upon multiple iterations and color applied to delineate 'within' and 'without' the Mandelbrot set, a bug is born, which will lead to a mass infestation of imaginations and knowledge |
And where the mathematics of complex numbers and iterations produce a mathematical reality visualized here in stereoscopic 3D film by Oldaker and Hart (2010) |
|
"The Mandelbrot set is a set of complex numbers, so we graph it on the complex number plane. However, first we have to find many numbers that are part of the set. To do this we need a test that will determine if a given number is inside the set or outside the set. The test is based on the equation Z = Z(squared) + C. C represents a constant number, meaning that it does not change during the testing process. C is the number we are testing, the point on the complex plane that will be plotted when testing is complete. Z starts out as zero, but it changes as we repeatedly iterate this equation. With each iteration we create a new Z that is equal to the old Z squared plus the constant C. So the number Z keeps changing throughout the test. We're not really interested in the actual value of Z as it changes, we just look at its magnitude. The magnitude of a number is its distance from zero. For example, the number -9 is a distance of 9 from zero, so it has a magnitude of 9. The magnitude of a complex number is harder to measure. To calculate it, we add the square of the number's distance from the x-axis (the horizontal real axis) to the square of the number's distance from the y-axis (the imaginary vertical axis) and take the square root of the result. In this illustration, a is the distance from the y-axis, b is the distance from the x-axis, and d is the magnitude, the distance from zero. As we iterate our equation, Z changes and the magnitude of Z also changes. The magnitude of Z will do one of two things. It will either stay equal to or below 2 forever, or it will eventually surpass two. Once the magnitude of Z surpasses 2, it will increase forever. In the first case, where the magnitude of Z stays small, the number we are testing is part of the Mandelbrot set. If the magnitude of Z eventually surpasses 2, the number is not part of the Mandelbrot set. The Mandelbrot set is an incredible object. It's really amazing that the simple iterated equation Z = Z(squared) + C can produce such beautiful works of mathematical art. " - David Dewey |
JULIA SETS
| in the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function. Informally, the Fatou set of the function consists of values with the property that all nearby values behave similarly under repeated iteration of the function, and the Julia set consists of values such that an arbitrarily small perturbation can cause drastic changes in the sequence of iterated function values. Thus the behavior of the function on the Fatou set is 'regular', while on the Julia set its behavior is 'chaotic'. The Julia set of a function ƒ is commonly denoted J(ƒ), and the Fatou set is denoted F(ƒ).[1] These sets are named after the French mathematicians Gaston Julia[2] and Pierre Fatou,[3] whose work began the study of complex dynamics during the early 20th century. |
- INCOMPLETE - IN PROGRESS ESSAY -
A.R. 2011
Saturna, Canada
Useful readings:
2020 illustrated essay on alchemy, visual alchemy and art:
'Alchemy, visual alchemy and their respective arts'
'Visual Alchemy in Theroy and Practice, and as Holographic Art'
|
A parallel universe: Sexuality and Eros - The Fuel of Visual Alchemies "Sexuality, eros, love and enchantment are part of the visual alchemies of our world. Whether expressed in the 'virtual' or 'real', whether invoking allegory or pure lust, it's basic resonance are the frequencies of life. Sex is part of alchemy, and part of everything else. : 'Projecting
- Desire' - lessons in the visual alchemies of projection
- Currently off-line - not for children or underaged readers |
Also re-visit surrealist and platonic
concepts in:
'Plato's
Cave and the Marvelous in Waiting'